Автор научной работы: » «Начала» геометрии многомерных измерений «
Михайлова Людмила Михайловна
Глава 1. Азы многомерной геометрии
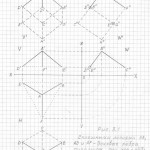
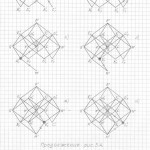
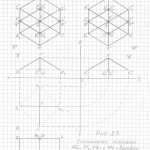
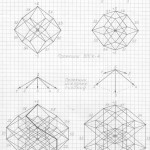
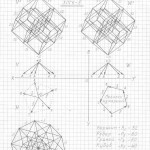
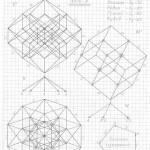
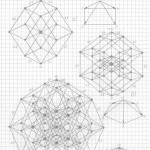
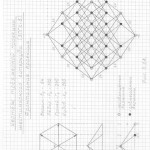
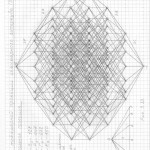
Глава 2. Трёхмерная проекция четырёхмерного гиперкуба (тессеракта)
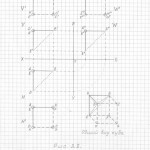
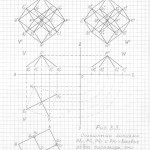
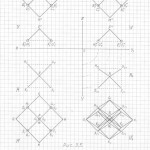
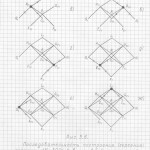
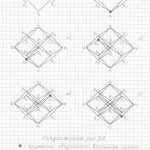
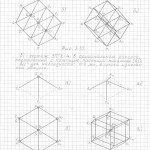
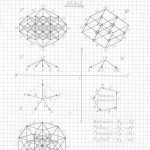
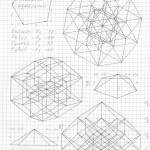
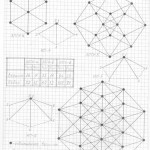
Глава 3. Универсальный метод построения (черчения) трёхмерных проекций гиперкубов любых измерений в любых проекциях и ракурсах
О РАБОТЕ: » «НАЧАЛА» ГЕОМЕТРИИ МНОГОМЕРНЫХ ИЗМЕРЕНИЙ»
Работа » «Начала« геометрии многомерных измерений» была написана с перепугу — боялась не успеть. Дело в том, что там, в Туркмении, у меня стало резко «скакать» давление, приходилось часто вызывать «скорую», и соседи, посоветовавшись, пришли спросить как и где меня хоронить. Я дала соседям деньги на свои похороны и попросила похоронить рядом с мужем.
Поэтому работа написана спонтанно, а сам изумительно простой «Универсальный метод построения (черчения) гиперкубов любых измерений в любых проекциях и ракурсах» был выявлен мною только в процессе написания этой третьей главы работы. Сейчас бы эту работу я написала бы по-другому, но, выехав из Туркмении, у меня почему-то пропало желание писать. Примите, пожалуйста, то, что написано.
Я — не профессиональный математик. Просто 2-го января 2003 года мне был такой «ЗНАК» : «Бог действует по геометрическим линиям.», и я тут же дала Богу обещание заняться математикой (мне было тогда почти 55 лет). И вот, чтобы не валяться, рыдая, на могилочке мужа, я ровно 8 лет и 1 день занималась математикой.
Уважаемые геометры!
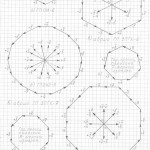
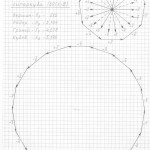
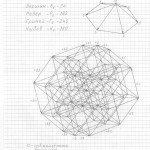
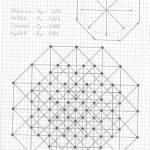
Пожалуйста, сначала примите, что все трёхмерные проекции гиперкубов любых измерений, как начерченные, так и созданные мною их модели из трубочек и лески, своей внешней геометрической формой напоминают детскую игрушку «юла, или волчок». И чем выше измерение, тем всё более и более трёхмерные проекции многомерных гиперкубов своей внешней формой принимают форму «юлы».
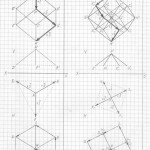
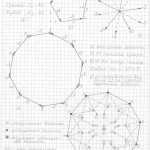
Вот теперь вам не составит труда геометрически изобразить «юлу» в любой проекции и в любом ракурсе. Надо только принять, что в теле «юлы» верхняя и нижняя часть — это конусы, а в телах трёхмерных проекций гиперкубов n-ного измерения эти «конусы» следует считать правильными n-угольными пирамидами (в работе я их назвала «исходными пирамидами».
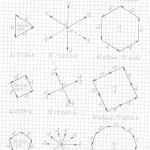
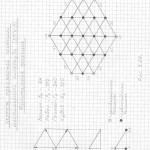
Правильная n-угольная пирамида состоит из n боковых рёбер, соединяющих вершину самой пирамиды с вершинами правильного n-угольника, являющегося основанием данной пирамиды. Так вот, эти » n боковых рёбер» и являются «рёбрами-измерениями» в любых трёхмерных проекциях n-мерных гиперкубов.
Причём, эти «исходные правильные n-угольные пирамиды» можно чертить абсолютно в любой проекции, в любом ракурсе, тогда составив (начертив) АБРИС (см. работу), вы легко начертите трёхмерную проекцию n-мерного гиперкуба в выбранной проекции, в выбранном ракурсе.
Желаю вам больших успехов.
С уважением,
Михайлова Людмила Михайловна.